题目链接
方法 1:前后缀分解
思路
- 计算 x 轴上每个单位可以接的雨水的大小,然后将他们累加起来。
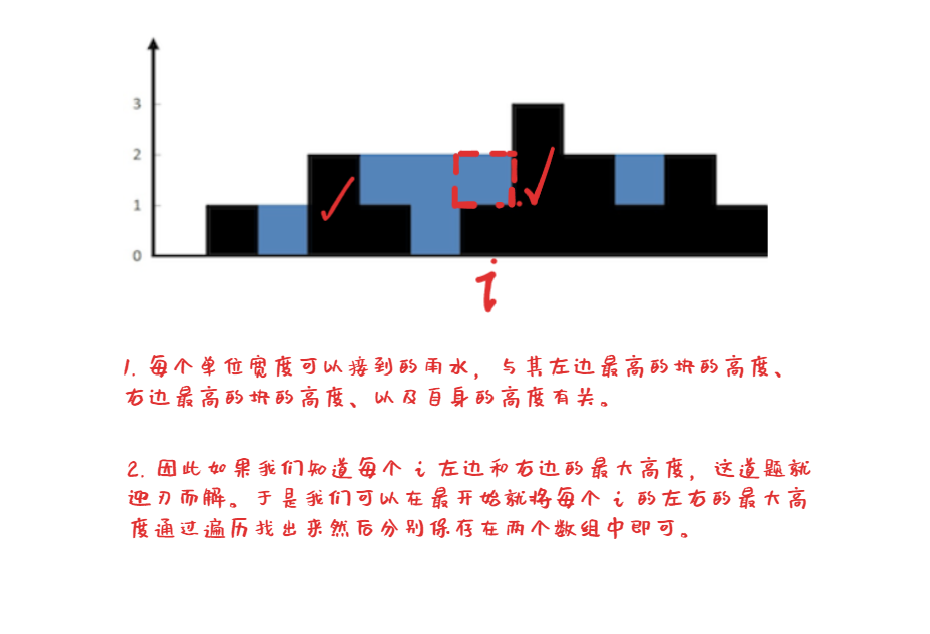
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
pre_max = [0] * n
suf_max = [0] * n
pre_max[0] = height[0]
for i in range(1, n):
pre_max[i] = max(height[i], pre_max[i - 1])
suf_max[-1] = height[-1]
for i in range(n - 2, -1, -1):
suf_max[i] = max(height[i], suf_max[i + 1])
ans = 0
for h, pre, suf in zip(height, pre_max, suf_max):
ans += min(pre, suf) - h
return ans
|
复杂度
方法 2:双指针(方法 1 优化)
思路
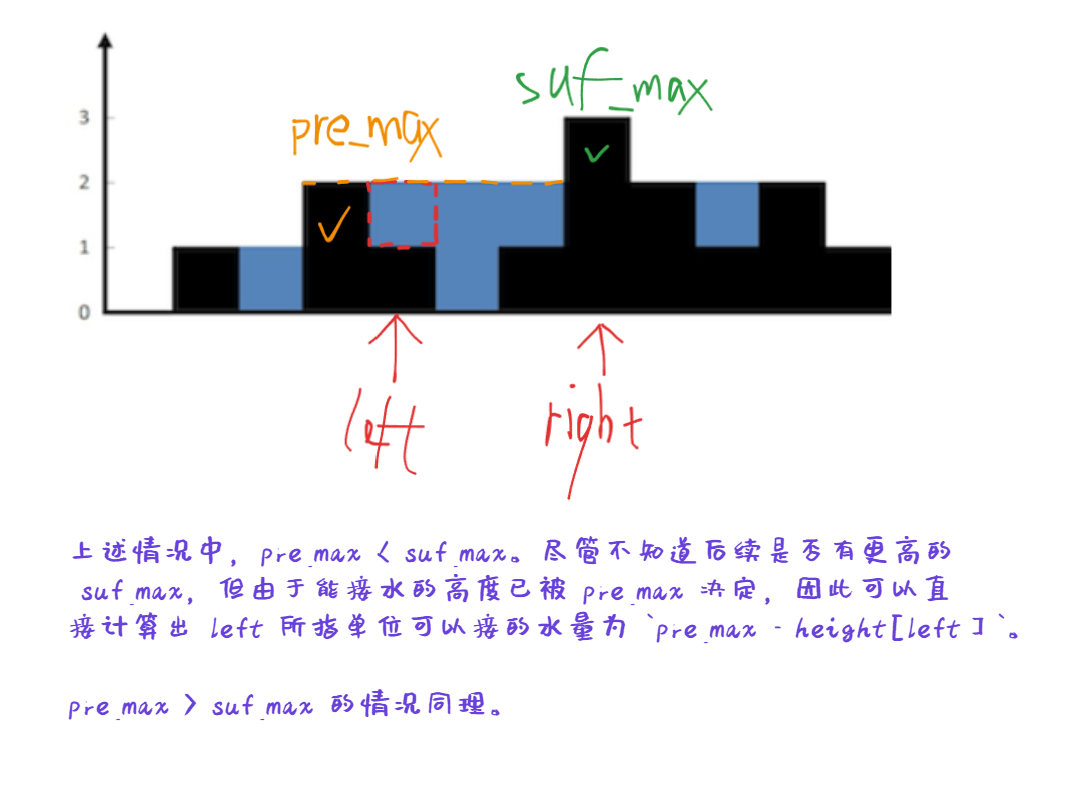
- 方法 1 中找两边最大高度,是为了找出两个高度中的较小值,然后以较小值为接水的高度计算答案。
- 既然如此,我们可以直接使用两个指针记录两边高度的最大值,哪边小了,就把哪边单位宽度可以接的雨水加上。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
pre_max = suf_max = 0
ans = 0
left, right = 0, n - 1
while left < right:
pre_max = max(pre_max, height[left])
suf_max = max(suf_max, height[right])
if pre_max < suf_max:
ans += pre_max - height[left]
left += 1
else:
ans += suf_max - height[right]
right -= 1
return ans
|
复杂度
方法 3:单调栈
思路
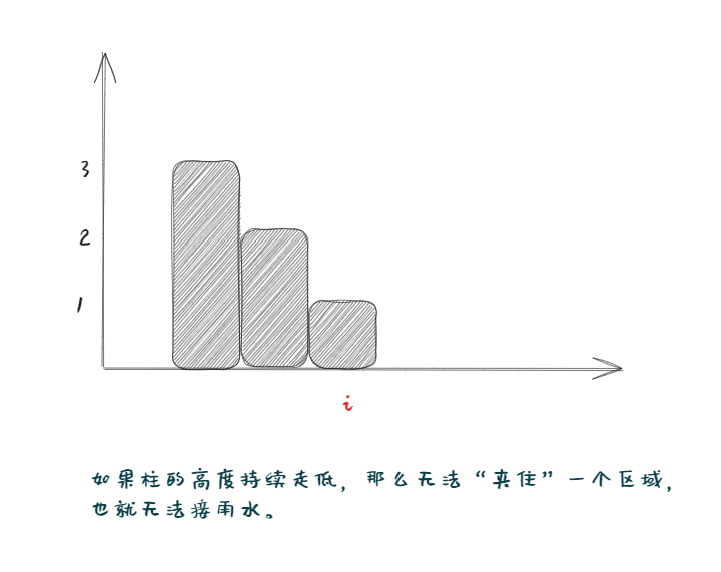
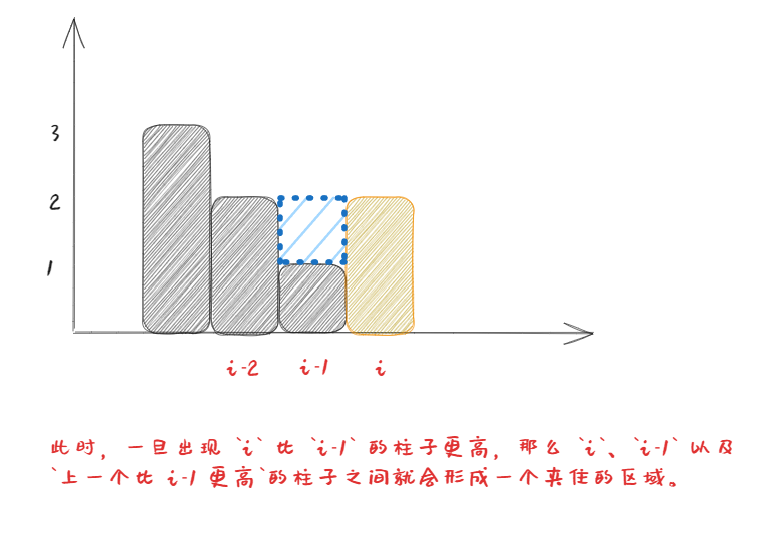
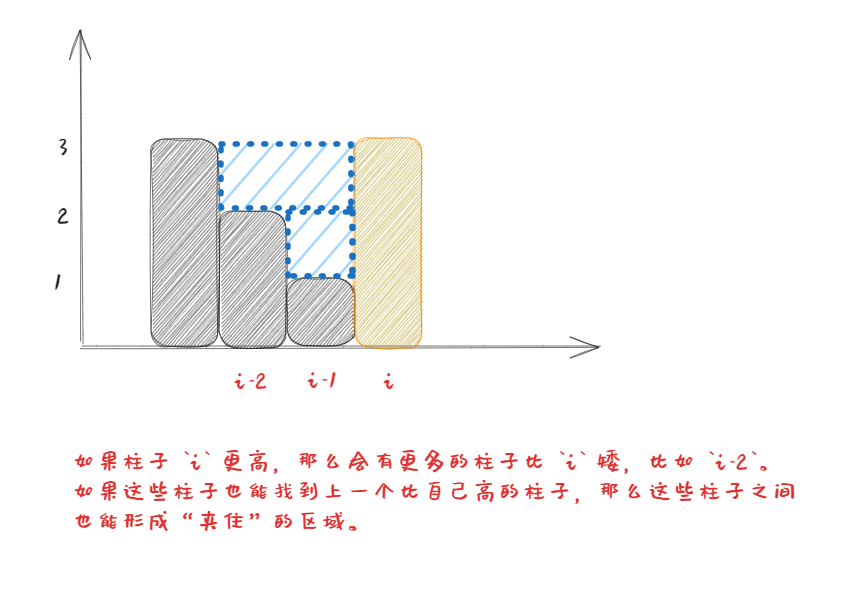
因此我们的策略为:
- 如果高度持续走低,我们就先入栈等待后续更高的柱子出现。
- 只要出现
i 比 i-1 更高,我们就可以开始依次往回计算 i 、i-1 以及 i-1 上一根更高的柱子夹住的区域可以接住的雨水的矩形区域面积了。把答案依次累加即可。
注意:“夹住”是需要区域的,因此 i 最近也只能和 i-2 才能计算面积。所以对于 i 来说,弹出一个柱子 i-1 之后栈空了,就没有能夹住的区域了,直接跳出循环即可。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution:
def trap(self, height: List[int]) -> int:
ans = 0
st = []
for i, h in enumerate(height):
# 如果一样高,也夹不住水,只保留最新的即可
while st and h >= height[st[-1]]:
bottom_h = height[st.pop()]
if not st:
break
left = st[-1]
dh = min(height[left], h) - bottom_h
ans += dh * (i - left - 1)
st.append(i)
return ans
|
复杂度




