题目链接

方法 1：前缀和

思路

1. 本题为前缀和数组的基础例题。通过构建一个前缀和数组，可以快速地求出任意两个区间的和。前缀和适合用在对于求区间和有需求的题目。
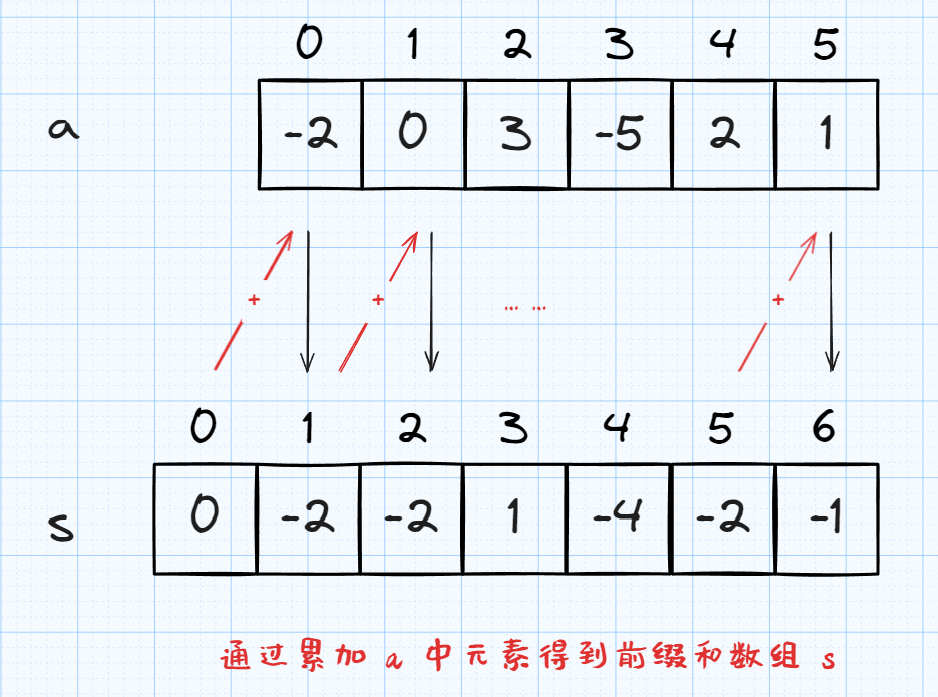
2. 设初始数组为 a，前缀和数组为 s。
   • len(s) = len(a) + 1
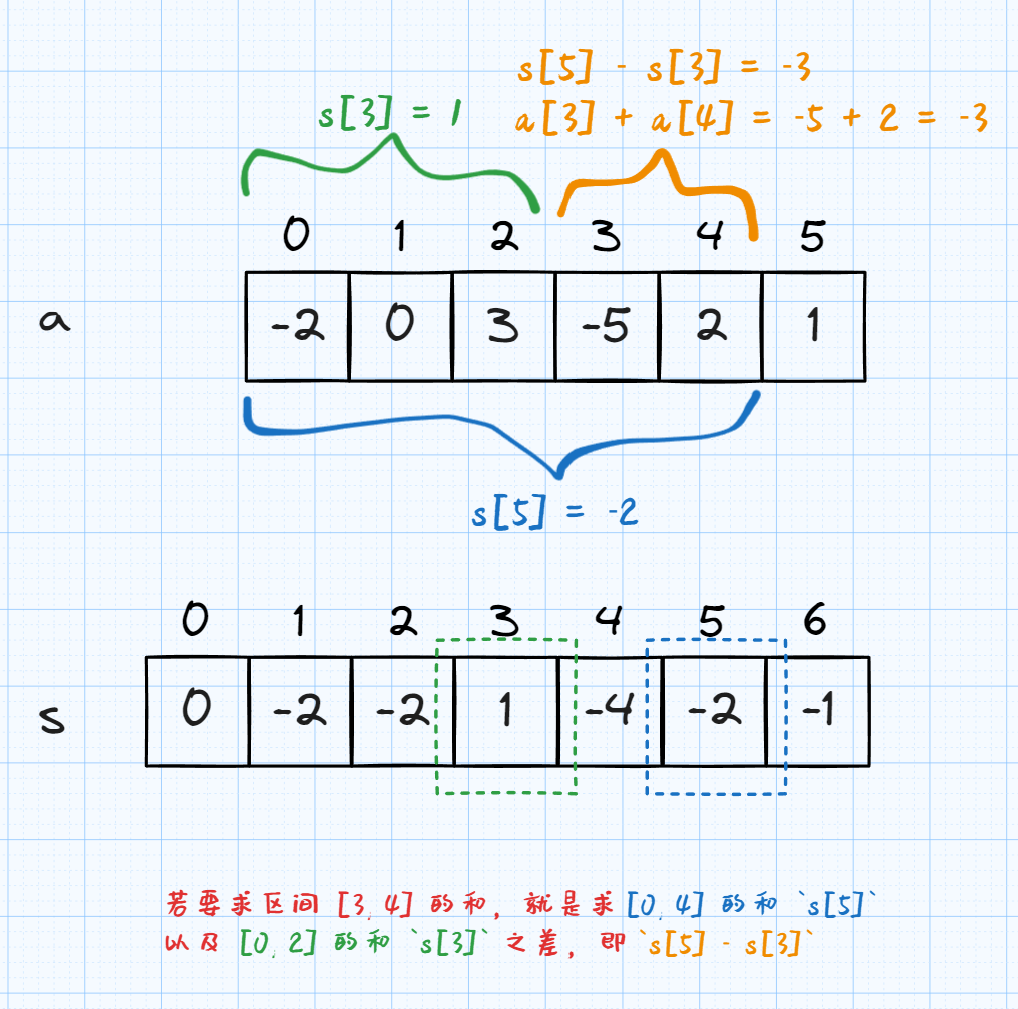
   • 我们令前缀和数组的元素 s[i] 的值为初始数组 [0, i - 1] 区间的元素之和，即 $$s[i] = \sum_{j = 0}^{i - 1}a[j]$$
   • 如此之后，求区间 [left, right] 之和，就是求 [0, right] 之和 - [0, left - 1] 之和，可以转化为求 s[right + 1] - s[left]。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class NumArray:

    def __init__(self, nums: List[int]):
        s = [0] * (len(nums) + 1)
        for i, x in enumerate(nums):
            s[i + 1] = s[i] + x
        self.s = s

    def sumRange(self, left: int, right: int) -> int:
        return self.s[right + 1] - self.s[left]

复杂度

• 时间复杂度：初始化 s 为 $O(n)$，sumRange 为 $O(1)$。
• 空间复杂度：$O(n)$。