15. 三数之和

方法 1：双指针

思路

遍历数组中的数固定为 i，在剩余未遍历的数中利用相向双指针 left 和 right 寻找 j 和 k。
每个指针都去重，则可保证答案中无重复数组。
利用极值进行剪枝优化。
注意不可以使用“固定 j，在两侧寻找 left 和 right 的方法，理由如下：

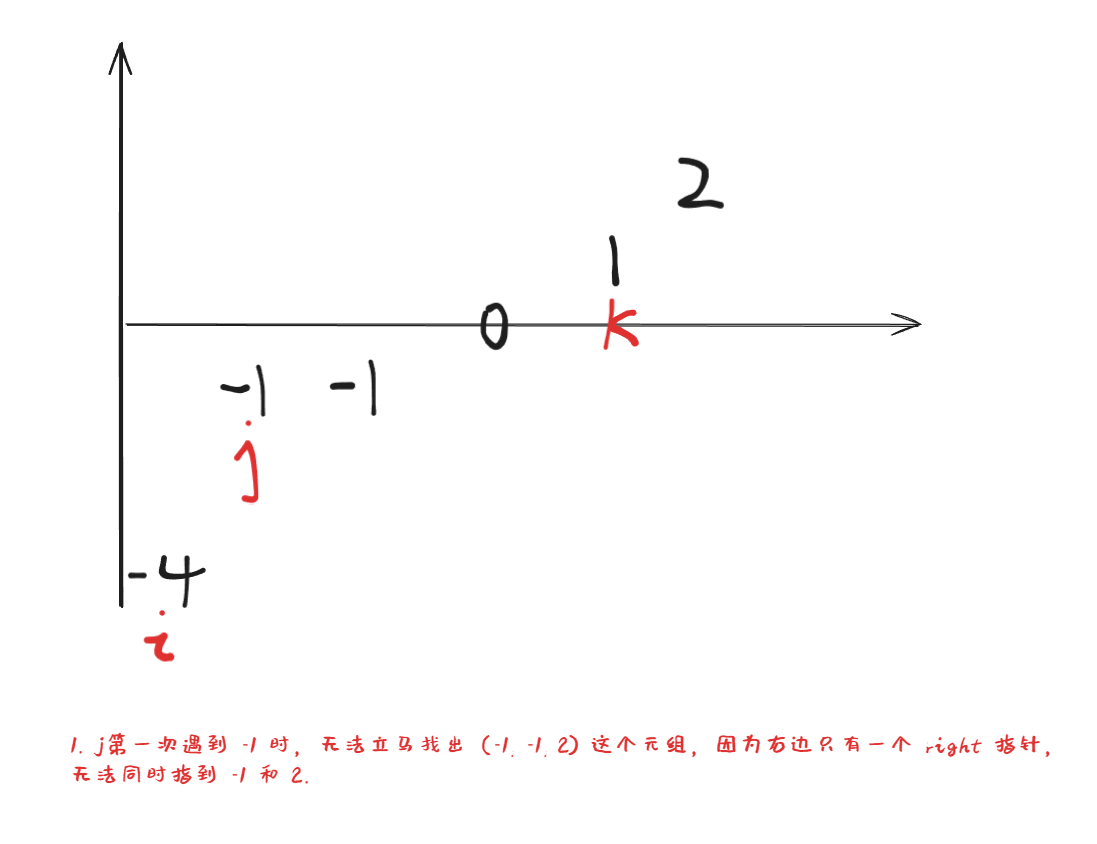
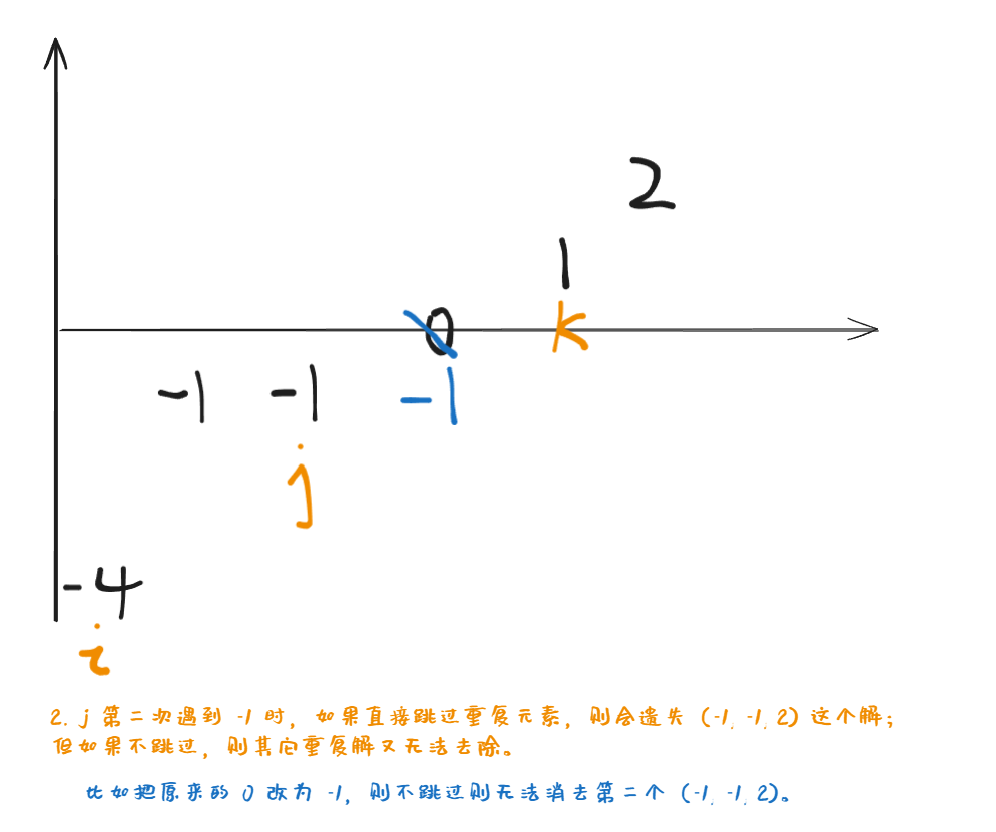
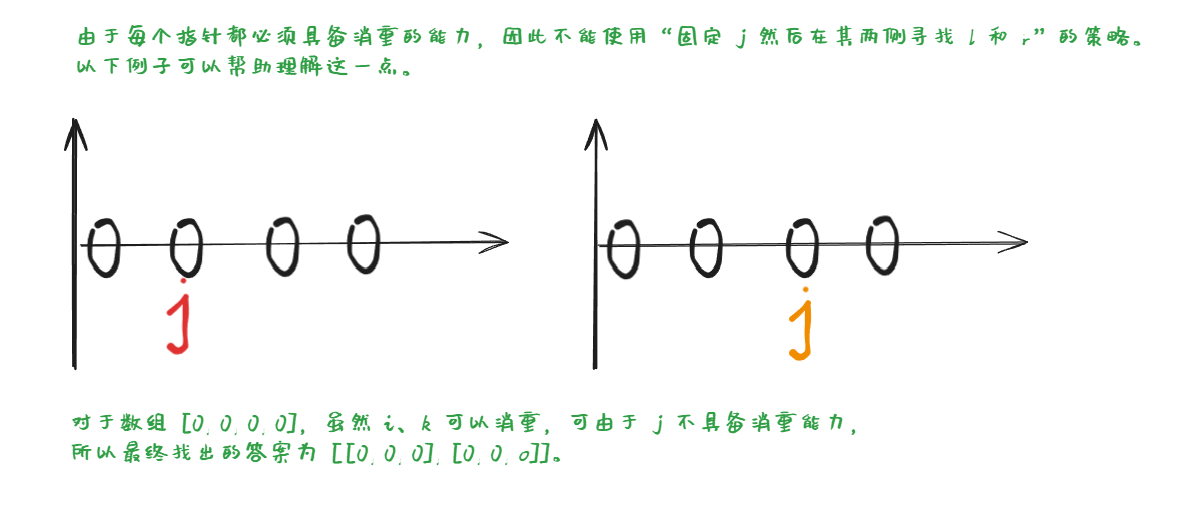
以下为以 j 为固定数的错误示例代码，可以自己拿去 leetcode 试验一下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()  # 先对数组排序
        ans = []
        n = len(nums)
        
        for j in range(1, n - 1):  # 固定中间的数 nums[j]
            
            l, r = j - 1, j + 1  # 左指针在 j 左侧，右指针在 j 右侧
            
            while l >= 0 and r < n:
                s = nums[l] + nums[j] + nums[r]
                if s == 0:
                    ans.append([nums[l], nums[j], nums[r]])
                    
                    # 找到一个解后，跳过重复的 l 和 r
                    while l > 0 and nums[l] == nums[l - 1]:
                        l -= 1
                    while r < n - 1 and nums[r] == nums[r + 1]:
                        r += 1
                    
                    l -= 1
                    r += 1
                elif s < 0:
                    r += 1  # 和小了，右侧指针向右移动
                else:
                    l -= 1  # 和大了，左侧指针向左移动
                    
        return ans

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()  # 先对数组排序
        ans = []
        n = len(nums)
        
        for i in range(n - 2):
            x = nums[i]
            if i > 0 and x == nums[i - 1]:
                continue
            if x + nums[i+1] + nums[i+2] > 0:
                break
            if x + nums[-1] + nums[-2] < 0:
                continue
            
            j = i + 1
            k = n - 1
            
            while j < k:
                s = x + nums[j] + nums[k]
                if s > 0:
                    k -= 1
                elif s < 0:
                    j += 1
                else:
                    ans.append([x, nums[j], nums[k]])
                    # 从下一个数开始去重
                    j += 1
                    # 最终需停在不重复的下一个数
                    while j < k and nums[j] == nums[j-1]:
                        j += 1
                    k -= 1
                    while k > j and nums[k] == nums[k+1]:
                        k -= 1
            
        return ans

复杂度

时间复杂度：$O(n ^ 2)$
空间复杂度：$O(1)$，不记入排序的栈使用。